图解密码技术 - 密钥
Contents
什么是密钥
密钥其实就是一个巨大的数字,在使用对称密码、公钥密码(非对称密码)、消息认证码、数字签名等密码技术时,都需要使用密钥。
数字本身的大小并不重要,重要的是密钥空间的大小,也就是可能出现的密钥的总数量,密钥空间越大,进行暴力破解就越难。另一方面,密钥空间的大小由密钥的长度决定。
密钥和明文是等价的,攻击者知道密钥、密文和加密方式后,就能知道明文。
信息的机密性不应该依赖于密码算法本身,而是应该依赖密钥。
各种不同的密钥
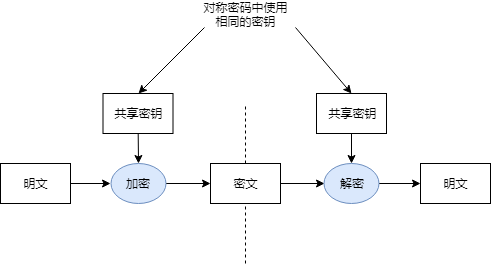
在对称密码中,加密和解密使用相同的密钥。
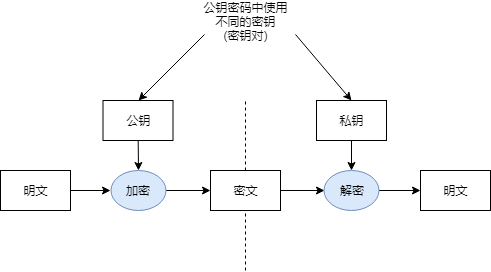
在公钥密码中,加密使用接收者的公钥,解密使用接收者的私钥。
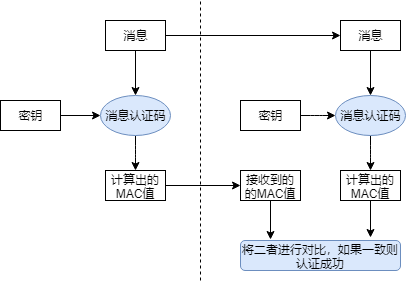
在消息认证码中,加密和解密使用相同的密钥。
在数字签名中,签名使用的是签名者的私钥,验证签名使用的是公钥。
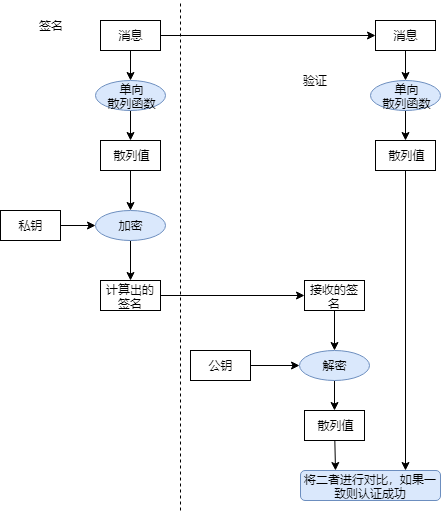
对称密码和公钥密码的密钥都是用于确保消息机密性的密钥,如果不知道合法的密钥就无法还原出明文。
消息认证码和数字签名的密钥适用于认证的密钥,如果不知道合法的密钥,就无法篡改数据,也无法伪装本人的身份。
CEK 和 KEK
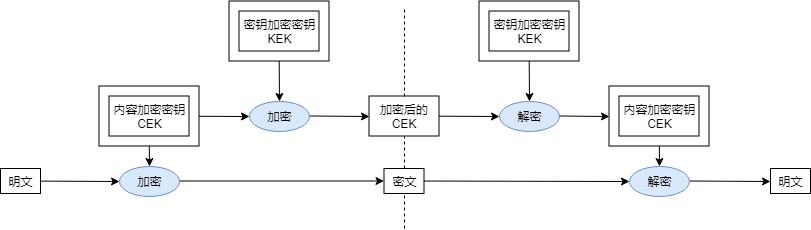
CEK(Contents Encryptiing Key)为内容加密密钥,加密的对象是用户直接使用的消息(内容)。
KEK(Key Encrypting Key)为密钥加密密钥,加密的对象是密钥。
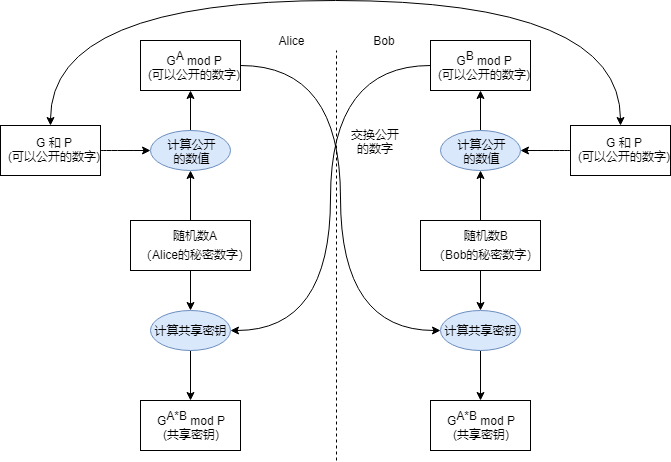
Diffie-Hellman密钥交换
Diffie-Hellman密钥交换(Diffie-Hellman Key Exchange)通过通信双发交换一些共有的信息,从而计算出一个公共的密钥。依靠数学计算的复杂度,来保证密钥的安全性。
假设Alice要和Bob通信,通过Diffie-Hellman密钥交换的过程如下。
Alcie向Bob发送两个质数P、G。
Alice生成一个随机整数A(1~P-2),A只有Alice知道。同时,Bob也生成一个随机整数B(1~P-2),同时也只有Bob一个人知道。
Alice发送$$G^AmodP$$的结果给Bob,Bob发送$$G^BmodP$$的结果给Alice。
Alice利用Bob发过来的结果计算共享密钥。$$key=(G^{B}modP)^{A}modP=G^{A*B}modP$$。
同理,Bob计算的共享密钥为$$key=(G^{A}modP)^{B}modP=G^{A*B}modP$$。
Alice和Bob可以轻松的计算出共享密钥,但是攻击者要从透露出来的消息计算出共享密钥则是十分困难的事情。