图解密码技术 - 公钥密码
Contents
密钥配送问题
在之前的对称密码模式中,加密和解密的密钥都是相同的,接收者必须收到密码和与之对应的密钥才能进行解密。在这一过程中,我们不能保证这个过程是否被劫持者劫持。
密钥必须发送,但又不能发送。这就是对称密码的密钥配送问题。
解决方法有以下几种:
- 通过事先共享密钥来解决
- 通过密钥分配中心解决
- 通过Diffie-Hellman密钥交换来解决
- 通过公钥密码来解决
前面三种方式都有各自的缺点,都不考虑。第四种方式通过公钥密码交换对称密钥为可行的方式。
公钥密码
公钥密码(public-key cryptography) 也称为 非对称密钥(asymmetric cryptography) ,加密和解密的过程分别由加密密钥和解密密钥来完成。发送者用加密密钥对消息进行加密,接收者用解密密钥对密文进行解密。
在公钥密码中,加密密钥一般是公开的,称为公钥(public key)。解密密钥是绝对不能公开的,称为私钥(private key)。公钥和私钥是一一对应的,称为密钥对(key pair)。
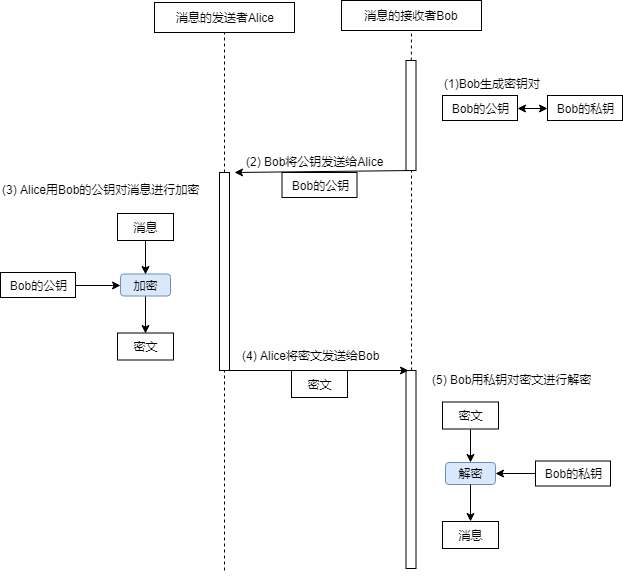
公钥和私钥一般都由接收者提供,接收者将加密密钥公开,这样任何人都可以通公钥对信息进行加密,但只有接收者才能通过私钥对加密后的信息进行解密。
简单的流程图如下所示。
RSA算法
RSA 是一种非对称加密算法,名字由它的三位创始人Ron Rivest, Adi Shamir, Leonard Adleman的姓氏首字母组成。
RSA可以被用于非对称密码和数字签名。
RSA加密和解密
在RSA中,明文、密文和密钥都是数字。
加密过程的公式如下所示。
$$ cipher = plaintxt^E;mod;N$$
简单来说,RSA的加密过程就是求明文的 E 次方 mod N,只要知道了E和N两个数,就能完成加密的运算。E和N的组合就是公钥(E,N)。
解密的过程和加密的过程一样。
$$ plaintxt = cipher^D;mod;N$$
解密的过程是求密文的 D 次方 mod N, 所用的密钥称为私钥(D,N)。
RSA生成密钥对
RSA的密钥对由E、D、N组成,(E,N)为公钥,(D,N)为私钥。
RSA的密钥对的生成步骤主要由一下几步完成。
求N
首先准备两个质数p、q,暂时选择17和19。
| |
求L
L为p - 1和q - 1的最小公倍数。
| |
求E
找到一个数E,使得E和L互质。
| |
满足条件的E有很多,例如:
| |
这里选择5作为E的值。
至此,得到了公钥(5, 323)。
求D
接下来求D,D要满足的条件是,E与D的乘积mod L的结果为1。即$$E * D;mod;L = 1$$。
当D = 29时,正好满足条件。
| |
模拟加密与解密
至此,我们已经成功得到了公钥对(E, N) = (5, 323)和私钥对(D, N) = (29, 323)。
这里要注意的是,要加密的明文必须小于323。因为如果明文大于N时,mod的结果必将小于N,这样的话,解密的结果也就必定小于N,无法还原出正确明文。
我们选择123作为加密的明文。
加密:$$plaintxt^E;mod;N=123^5;mod;323=225$$
解密:$$cipher^D;mod;N=225^{29};mod;323=225^{10}225^{10}225^{9};mod;323=1616191;mod;323=123$$
总结起来,求密钥对的过程可以由下表表示。
| 步骤 | 过程 |
|---|---|
| 求N | 用伪随机数生成器生成质数p和q,N = p * q |
| 求L | L 为 p -1 和 q - 1 的最小公倍数,L = lcm(p - 1, q - 1) |
| 求E | E 和 L 互质,并且1 < E < L, gcd(E, L) = 1 |
| 求D | E 和 D mod L = 1,并且1 < D < L,E * D mod L = 1 |
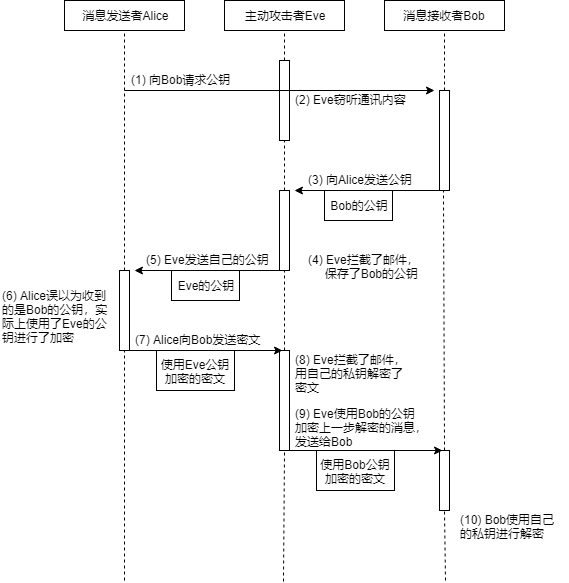
对RSA的攻击
对RSA的攻击主要还是中间人的方式。其他的攻击方式都很难实现。